Green’s functions

For the self-consistent solution algorithm of the Green’s functions, self-energies, and electrostatic potential, see NEGF formalism.

Steady state assumption

—

Axial energy cut-off

Heterostructures consist of a large number of subbands, but only a few near the band gap are relevant for the electronics and optoelectronics (Figure 4.2.2 left). nextnano.NEGF therefore selects a limited number of subbands and construct the Green’s function basis (Figure 4.2.2 right).

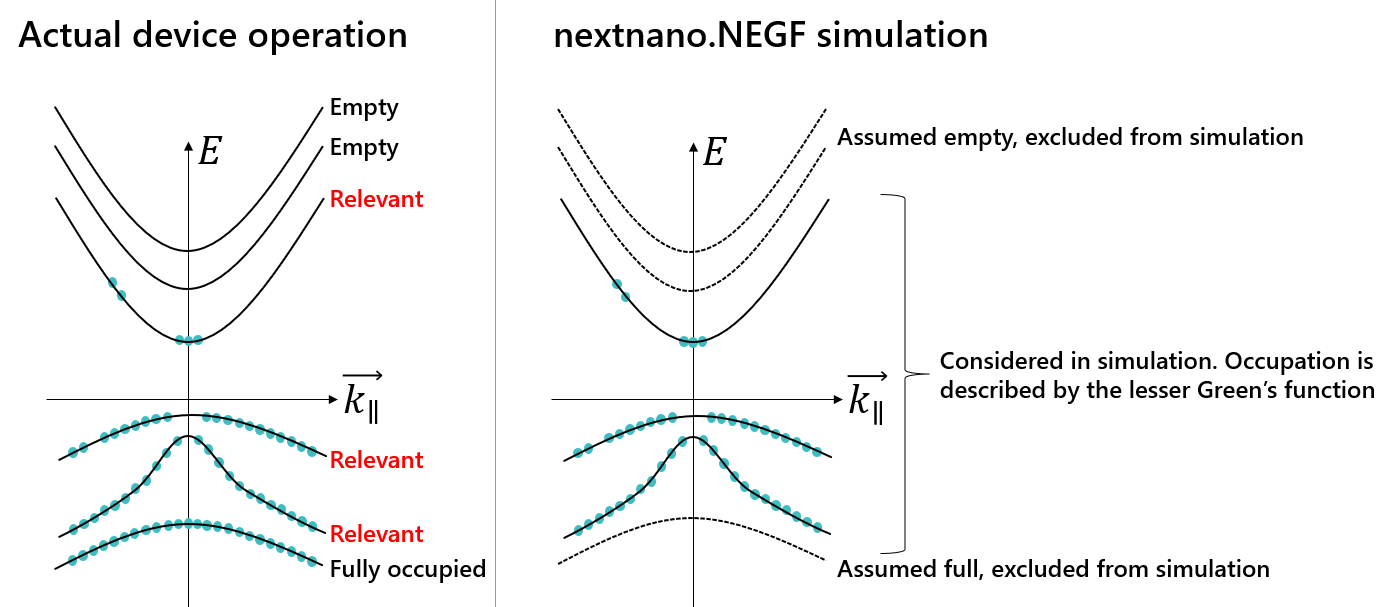
Figure 4.2.2 Schematics of miniband selection in the “electron picture”, in which the valence band is regarded as an almost fully-occupied sea of electrons.

You can specify the cut-off either by the energy range measured from the ground states (EnergyRangeAxial and/or EnergyRangeAxialValence), or by the number of subbands (NumberOfConductionSubbands and/or NumberOfValenceSubbands). The number of subbands is considered to be without the spin degree of freedom.

Reduced real space basis

The ‘reduced real space’ modes are the eigenstates of the position operator in the reduced Hilbert space (i.e. after Axial energy cut-off). Because of the energy cut-off, these states are spatially broadened instead of being the delta functions. These position eigenstates are used as a basis in the NEGF calculation. It does not depend on the applied voltage. However, this basis has generally little use in terms of physical interpretation.

Energy range of the Green’s functions

Per default, the energy range of the Green’s functions are set automatically considering the ground state energies of the electrons, axial and in-plane energy ranges, and the bias.

However, occasionally, this default energy range needs to be modified by setting EminShift and/or EmaxShift. Please check the output of the spectral function and carrier densities to know whether the default setting of the energy range of the Green’s functions is sufficient. Since September 2024, a warning is raised if the energy range may be insufficient.

For example, the lower edge of the energy range is too high in Figure 4.2.3.

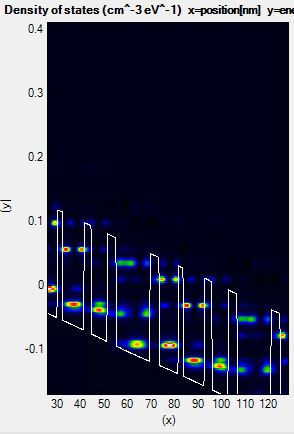
Figure 4.2.3 Density of states of a QCL calculated with a non-ideal energy range.

When we shift EminShift by 50 meV, it gives a better convergence and more accurate results in Figure 4.2.4.

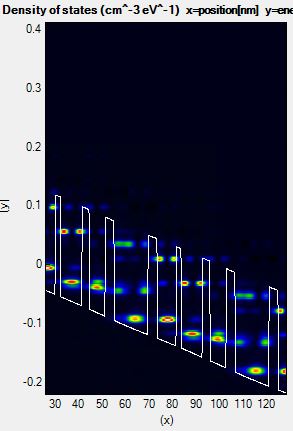
Figure 4.2.4 Density of states of a QCL calculated with too high energy maximum.

Yet, the upper edge goes far beyond the highest density of states available in the simulation (which is limited by Axial energy cut-off). By setting EmaxShift to -250, the calculation becomes faster while correctly accounting for the relevant energy range:

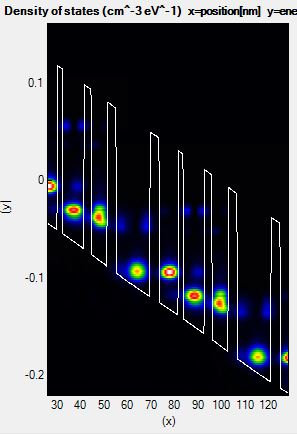
Figure 4.2.5 Density of states of a QCL calculated with a good energy range.

Relation to physical quantities

The electron density is related to the lesser Green’s function:

\[n(z, E_z) = - \frac{i}{2\pi} G^<(z, z' = z, E_z)\]

The local density of states is related to the spectral function:

\[g(z, E_z) = \frac{1}{2\pi} A(z, z' = z, E_z)\]

where \(A = i(G^\mathrm{R} - G^{\mathrm{R}\dagger}) = -2\mathrm{Im}G^\mathrm{R}\). \(G^\mathrm{R}\) is the retarded Green’s function.

Coherence length

Unless you specify an open system using Hybrid{ }, the code uses field-periodic boundary condition. In this way the simulation accounts for an infinite periodic structure, with a periodic electric field. Coherent transport between the central and \(N\)-th adjacent periods is considered, where \(N\) is set by CoherenceLengthInPeriods.

Note

Limiting the coherence length will speed up the calculation of the self-energies. On the other hand, this can reduce the accuracy of the scattering processes if this length is below the actual coherence length in the simulated device. It is recommended to asses the accuracy of such approximation by comparing to the results for different values of this coherence length to the full calculation.

---

Last update: 08/11/2024