— FREE — Surface Charges

Header

Files for the tutorial located in nextnano++\examples\basics

• contacts_1D_zero_field_surface_charges_GaAs_nnp.in

• contacts_1D_zero_field_surface_acceptors_GaAs_nnp.in

Scope:

Surface charges on boundaries - comparison to the Schottky barrier

Interface charges (surface states)

Instead of specifying a Schottky barrier, the user can alternatively specify a fixed surface charge density as presented in contacts_1D_zero_field_surface_charges_GaAs_nnp.in. The use of charges is similar as of dopants. One needs to define them for a specific region

structure{
    ...
    region{ # interface charges (surface states)
        line{ x = [10 , 10 + $Width] }
        doping{
        constant{
            name = "negative-interface-charge"   # name of impurity
            conc = $VolumeDensity                # doping concentration [cm-3]
        }
    }
}

and define with some name and given sign.

impurities{
    ...
    charge{
        name = "negative-interface-charge"          # refer to region with name negative-interface-charge
        type = negative
    }
}

Figure 2.4.30 shows that the red curve ( = “ohmic” contact with interface charge density \(\sigma\) (surface states) of -8.4796 \(\cdot\) 10¹² \(|e|\) /cm² = -1.3586 \(\cdot\) 10^-2 C/m²) is equivalent to the black curve (Schottky barrier of 0.53 eV).

A sheet charge density of -8.4796 \(\cdot\) 10¹² cm^-2 corresponds to a volume charge of -8.4796 \(\cdot\) 10²⁰ cm^-3 if one assumes this charge to be distributed over a grid spacing of 0.1 nm. In this case, the interface charge density corresponds to a Neumann boundary condition for the derivative of the electrostatic potential \(\phi\):

\[\frac{d\phi}{dx} = - E_x = \mathrm{const},\]

where \(E_x\) is the electric field component along the x direction. \(E_x\) is related to the interface charge as follows:

\[E_x = \frac{\sigma}{\epsilon_r\epsilon_0}\]

where \(\epsilon_0\) is the permittivity of vacuum and \(\epsilon_r\) is the dielectric constant of the semiconductor. In this example:

• \(\epsilon_r\) = 12.93 for GaAs

• \(E_x\) = 1049.7 kV/cm

The output for the electric field (in units of [kV/cm]) can be found in this file: electric_field.dat

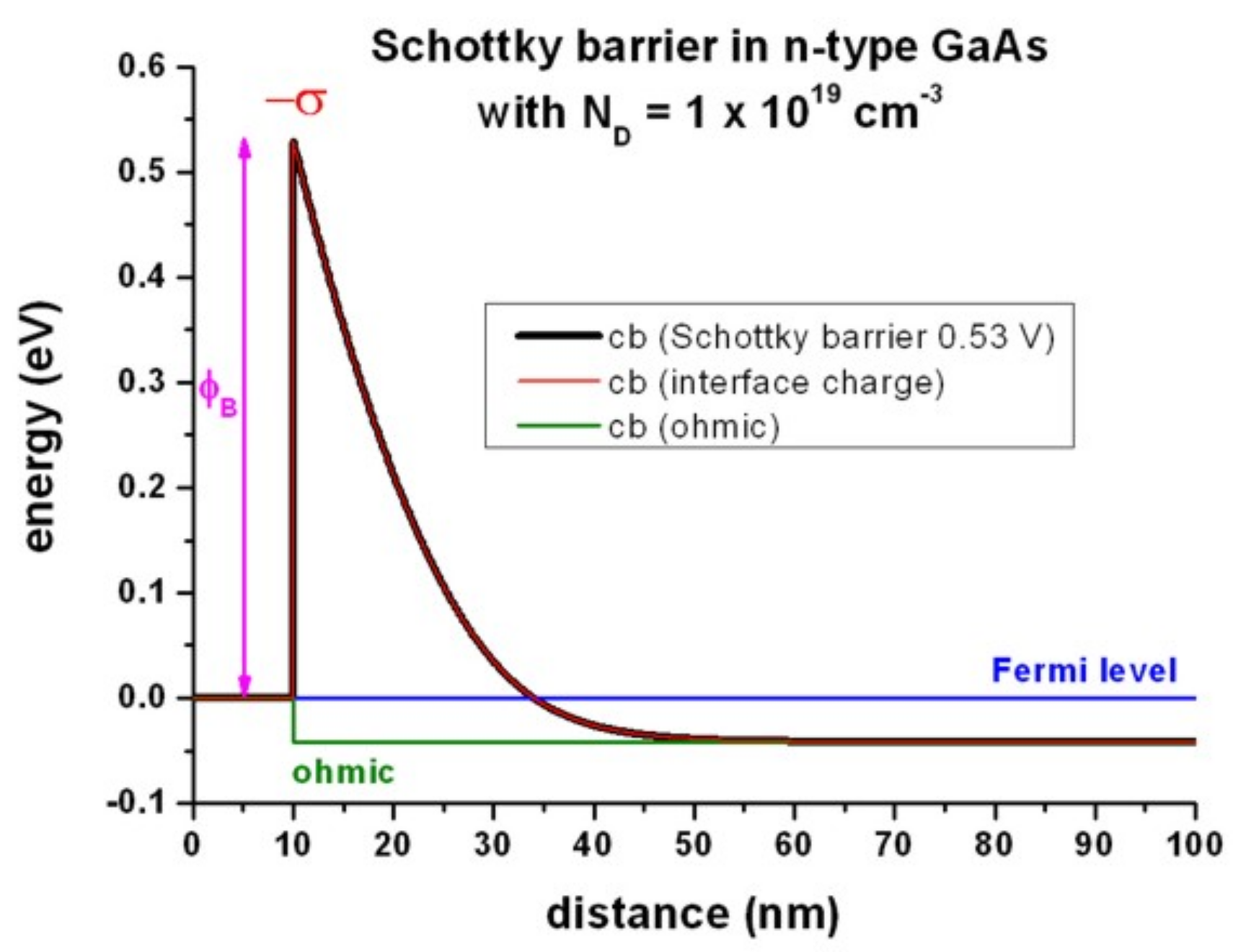
Figure 2.4.30 Calculated conduction band profile

The output for the interface densities can be found in this file: material\density_fixed_charge.dat.

Surface states - Acceptors

Input file: 1DSchottky_barrier_GaAs_surface_states_acceptor_nnp.in

Instead of specifying a Schottky barrier, the user can alternatively specify a density of acceptor surface states (p-type doping). Essentially, this can be done by specifying a p-type doping region that is very thin, i.e. the doping is specified only on one grid point.

In this example, we use a doping area of 0.1 nm at the surface that we dope p-type with a volume density of 847.96 \(\cdot\) 10¹⁸ cm^-3. This corresponds to a sheet charge density of 8.4796 \(\cdot\) 10¹² cm^-2 where we assume the states to have realistic activation energies.

impurities{
    ...
    acceptor{ # p-type
        name = "impurity_p"
        energy = 0.027 # p-C-in-GaAs (Landolt-Boernstein 1982)
        degeneracy = 4 # degeneracy of energy levels, 2 for n-type, 4 for p-type
    }
}

The results are the same as shown in Figure 2.4.30 for the interface charges.

Last update: 16/07/2024